Related pages on Antennas , radiation and fields , mobile and short verticals
My 2004 Dayton Hamvention Power Point presentation on Small Verticals can be downloaded here... DAYTON 2004.
When dealing with small antennas, the main points to remember are:
The steps outlined above maximize radiation resistance and minimize loss. Let's look at the interaction between radiation resistance and loss resistance.
Radiation resistance is both the most useful and the least useful antenna-related term. Radiation resistance can easily be misused and rendered useless. This is because radiation resistance has multiple poorly-defined meanings. When a term has several nebulous meanings or uses, it is only natural that misuse or mixing of terms appear. Lack of a firm, single, well-accepted, definition allows the term "radiation resistance" to slip from one definition into another. This often results in well-intentioned, but totally erroneous conclusions, that seem to follow accurate, logical, thought!
There are two commonly-used "correct" meanings of radiation resistance, and one totally incorrect use. The "correct" uses are:
The resistive part of an antenna's feedpoint impedance that is created solely by radiation from the antenna (This is the feedpoint resistance less and loss resistances in the system)
The total power radiated in all directions divided by the square of maximum net (or effective) current causing the radiation (This is the IRE definition)
Neither of the above definitions include loss resistances of any type! The moment loss resistance is included, we have a third commonly-used (but totally useless) definition. This definition, which includes losses, could be considered "incorrect" because it includes resistances that have nothing to do with radiation. The misused, or nearly useless, definition is:
3. The simple real (or resistive) part of an antenna's feedpoint impedance, irrespective of whatever the feedpoint is in relationship to the radiating current maximum or any losses.
The correct name for numbers 1 and 3 "radiation resistance" are actually the antenna feedpoint resistance. They do not show the real radiation resistance!
Of the above good or useful definitions, the first definition is most commonly abused through mistake. The second definition is an IRE definition (albeit a good one that never caught on). In every case, the second good definition, which is also the least commonly used, provides the most direct and useful answer.
In order to understand what is right, we sometimes have to learn what is wrong. Let's look at a few examples where radiation resistance is misused to give nonsensical answers.
Folded monopoles provide the clearest common example of radiation resistance misuse. Quite often, in discussions of vertical antenna ground system loss, claims are made that multiple drop wires increase radiation resistance and lower earth or ground system losses. The justification is multiple drop wires, or a folded monopole element, increases radiation resistance. The increased radiation resistance reduces ground currents and ground losses. This concept is justified and/or rationalized through use of another commonly misused and abused formula: eff % = 100 * Rrad/(Rrad + Rloss) .
In order to use the formula above, all losses must be normalized to the same point where radiation resistance is taken. Without doing that, the efficiency formula above does not work! Many articles, especially folded monopole articles, either ignore the fact that loss resistances must be normalized to the feedpoint, or authors are unaware of that fact.
Let's look at what actually happens in a folded element, and use it to understand how the poor definition of radiation resistance causes efficiency misunderstandings.

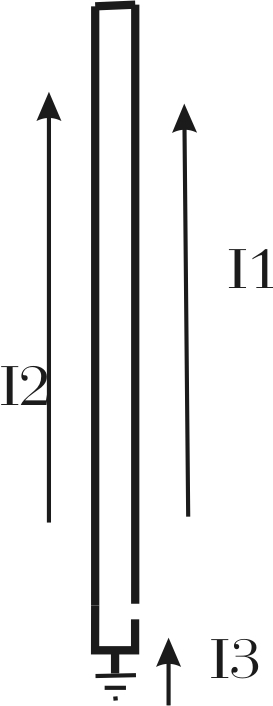
Consider the unipole to the left. Let's assume it is 1/4 wavelength tall. Let's assume we short or close the open gap and feed it as a normal 1/4 wave Marconi vertical with a feedpoint at the point where I3 is shown. I3 is ALWAYS the vector sum or in-phase combination of currents I1 and I2. With continuity through each leg, I1 and I2 equally share all of the ground current. This happens regardless of where the feedpoint is located in the lower portions of the antenna.
With 1/4-wl height and with a reasonable element diameter, the radiation resistance (fed as a traditional monopole) would be about 36-ohms. Let's assume ground loss, normalized to the point where we measure I3, is14 ohms.
Applying 500 watts makes I3 a current of 3.16 amperes. Power loss in ground resistance would be I^2R, or 3.16^2 times 14, about 140 watts. Feedpoint resistance would be 50 ohms. Feedpoint power, as a check, would be 3.16^2 times 50 ohms or 500 watts. With equal diameter legs, this current would divide and 1.58 amperes would flow in each upper leg at I1 and I2.
Let's use the formula eff %= 100*Rrad/(Rrad+Rloss). We have 36/36+14 = .72 so the result is 72% efficiency, or 28% loss. 28% loss times 500 watts is 140 watts in ground losses. This matches the other method just above.
Opening the gap and feeding as a folded unipole, half of the radiator current is in I1 while the other half is in I2. Current is halved to 1.58 amperes at the feedpoint and power remains the same. The feedpoint resistance now becomes 200 ohms. We can confirm this with I squared R, or 1.58^2 *200=500 watts. It all works out great so far!
Now let's misuse the same efficiency formula, like Bill Orr did in his Radio Handbook and others do in various articles. We have 200/200+14 = .9346 or 93.46 % efficiency. It seems by using the folded monopole element we have increased efficiency from 72% to 93.5%!
We know we still have 3.16 amperes flowing as I3, and we know ground resistance is still 14 ohms (normalized to the point where I3 is measured). I-squared-R losses are 3.16^2 * 14 = 140 watts! We have exactly the same power loss in the ground.
Let's transform the ground loss value that was normalized at 14-ohms where I3 is measured to the feedpoint by the same impedance multiplication as the feed resistance, or 1:4. We'd now have a normalized ground loss resistance of 4*14 = 56 ohms. 56 ohms of the 200-ohm feedpoint resistance is loss. Trying that same efficiency formula, we get:
144/144+56 = .72, or 72% efficiency!!! Now everything checks out fine.
Many people use the first definition of radiation resistance, the portion of the terminal resistance of the feedpoint responsible for radiation. Unfortunately they fail to normalize ground losses to the same point where the radiation resistance is taken! We can not use a formula that is based on everything being normalized to one point and not normalize to that point for every term in the formula! There is no change in efficiency when the NET radiator current remains the same and when net ground current remains the same. Without changing power dissipated in losses compared to power radiated, we can move the feedpoint resistance all around to anything we like and efficiency remains the same.
Even if used properly, in many cases, losses are external to the antenna system. These losses appear exactly as if they are due to radiation. For example, a Marconi vertical can be -5 dB down from theoretical due to losses out in the Fresnel region, or from local induction field dissipation, and not appear to have an abnormally high feed resistance.
To know efficiency and field strength, we really must measure field strength!
If we use the second definition of radiation resistance, the one defined years ago by the IRE, where the effective current causing radiation is compared to power radiated, we find folding the element does not change efficiency. Using the IRE definition of radiation resistance, a folded dipole or monopole has the same radiation resistance as a regular dipole or monopole the same size. Using the IRE definition, a small loop antenna has the same radiation resistance regardless the number of turns. All of this fits perfectly with real life antennas.
Using the IRE definition, the magic "free lunch" vanishes.
You can read about this in textbooks. The "Antenna Engineering Handbook" by Jasik in 3-13, 19-3, and in other sections uses correct definitions and descriptions.
We find the same efficiency misconceptions in articles about small loops and large quads. Authors sometimes assume, incorrectly, radiation resistance changes in a favorable proportion to loss resistance as feed impedance increases. What we really are doing is placing the feedpoint in series with a smaller portion of NET current causing radiation. The quad antenna has two current maximums, and the feed line only connects to one of them.
With a large full-size quad element the pattern under some conditions will slightly change, but efficiency remains basically the same. With a small "magnetic" loop antenna, losses usually increase with more turns! This is why most commercial transmitting loops only have a single turn.
Folded Dipoles
Folded dipoles, like folded monopoles, are another example of a system where radiation resistance can have two significantly different values, depending on which definition is used.
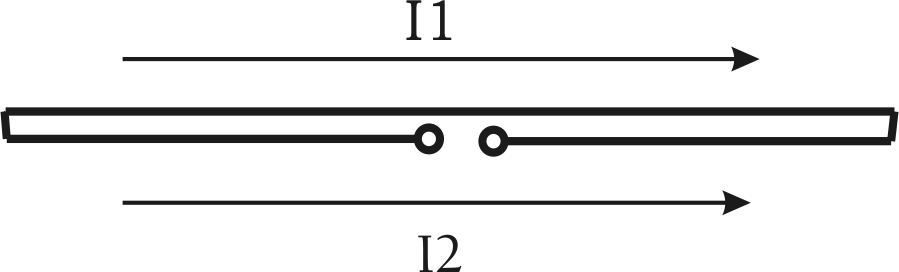
As with the monopole, the folded dipole only has half of the normal dipole current in each conductor. The sum of I1 and I2 is identical to a simple traditional dipole. Using the IRE definition of radiation resistance, freespace radiation resistance of a thin folded dipole is approximately 73 ohms. Using the less useful feedpoint resistance method, radiation resistance would be approximately 292 ohms. Some engineering books use the IRE definition, and clearly state a folded dipole has about 73 ohms radiation resistance, while other less-profession texts use the real part of feedpoint resistance.
In amateur circles, the Coaxial Dipole (or Double Bazooka) misuses the formula eff % = 100 * Rrad/(Rrad + Rloss) to claim the coaxial dipole or double bazooka has gain over a regular dipole. This is one of the most abused formula in articles.
Another abuse of radiation resistance is found in terminated antennas. Some manufacturers and authors claim a resistance can be inserted in series with one leg of a folded monopole or folded dipole, and the other leg fed. The usual arm-waving claim is the antenna isn't really resistor loaded, and that efficiency is very good because radiation resistance is high. Once again the claim is incorrect, and the root of the problem is not normalizing losses to the feedpoint.
A large terminated rhombic is well-known to have poor efficiency. Rhombic gain is actually low compared to other antennas having the same sin/sin x antenna pattern, because rhombic efficiency is generally less than 50%. At least half of the power is consumed in termination and ground losses below the antenna. The actual gain may be reasonably high compared to a dipole, but not to other efficient antennas with the same half-power beam width.
The typical manufacturing buzz-word is that terminated monopole and dipole antennas are "traveling wave antennas" and by some magic (that even large terminated rhombic antennas can't achieve) have broad bandwidth and very high efficiency.
A rhombic focuses energy (that is not transformed into heat) into a narrow beam that has considerable gain, but if it sprayed the radiation around in a non-focused pattern, a regular dipole would win hands down. Throw a resistor on that dipole to smooth SWR variations, or on a vertical, and efficiency suffers. I listened to a station on 75 meters 600 miles away testing a Sommer T-25 vertical. He was 30 over nine using a dipole, and dropped to S6 with the vertical. The European he was working reported a similar change. By removing the termination resistor and base-loading the same vertical, a local Ham gained almost 25dB on 80 meters!
When we abuse or misuse radiation resistance, we can invent all kinds of magical antennas. We can have CFA's, E-H antennas, fractal loops, terminated dipoles, small magnetic loops, and verticals with all sorts of magical claims. Few, if any, of the claims are ever correct. Any time we see a claim that efficiency changes a large amount because of a feed method change, or that an antenna makes exceptional efficiency without proper supporting field strength measurements, it should be a red flag.
Radiation resistance, at least under the useful IRE definition, can be defined by the following formula:
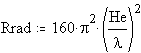
which would translate to:
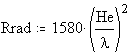
Where He is the effective height center of accelerating charges that cause radiation. In other words, He is the effective height, expressed in fractions of a wavelength, of the distributed common-mode