Gain does not come from antenna area or size.
Aperture
is a function of gain, gain is not a function of aperture. Gain comes
from compressing
radiated power into a
narrower area without increasing losses more than the compression or focusing
increases directivity.
One
analogy is a
balloon. Consider the air (or better a liquid like water that cannot compress)
inside the balloon as the power. If we
half-fill a
perfectly round
balloon with a given
volume of uncompressible liquid and
squeeze it, the
balloon extends out
in other directions. We have not increased liquid volume inside the balloon, we
just made it extend more in one direction at the expense of other directions.
An antenna works in
a similar manner.
Our transmitter's
power fills space in multiple directions, and we
modify or build the antenna
in a way that causes
transmitter power to
"fill less space area", hopefully only removing energy from
unwanted directions. While the
total power radiated
does not increase
(the net radiated
power can never be
more than the
applied power),
power density in certain
directions increases. This
assumes of course we
don't do something
foolish or harmful while
squeezing the
pattern, causing
transmitter power to
be dissipated as
heat.
We do something
to force radiation
into a smaller volume of
space without adding
significant
additional heat
loss, and we
suddenly have
"gain".
Gain is
always defined a
ratio of the antenna
under test to the level from some other known radiator. Models commonly a
(fictitious) isotropic
radiator (commonly in a model),
because models know how much power is applied. When dealing
with realworld
measurements, we
almost always use
a reference dipole
at the same mean
height. If we do not use a dipole reference, we use and specify some other known
reference antenna.
The "add 2.15 dB to isotropic" rule works in freespace when comparing antennas in freespace, but it does not work when an antenna is placed over earth. The instant the earth is involved in a model or measurement, the 2.15 dB rule flies out the window.
Why? Because there is no such thing as isotropic radiation over earth! We cannot have an isotropic pattern when something is distorting the pattern, and earth seriously changes the pattern (and gain). This isn't saying we cannot use dBi, we just have to be extra cautious when earth or other things are involved.
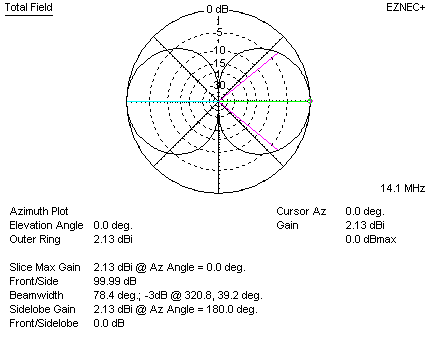
As a basic starting point let's look at dipole gain in freespace dBi:

Freespace gain of a low-loss dipole is 2.13 dBi.
This gain occurs because the dipole compresses the pattern into a "figure 8". In some directions (directly off the ends of the dipole) there is virtually no radiation at all. All low loss dipoles with proper feed, regardless of frequency, have about 2.15 dBi gain.
Now let's put a dipole antenna model over real earth 1/2 wavelength above flat ground:
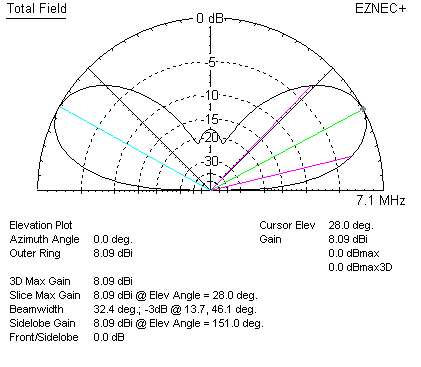
We see now the gain is 8.09 dBi. This is because the earth compresses the pattern vertically. Gain would actually be more than 8.1 dBi, except the model uses fairly low conductivity earth. There is actually 0.67 dB of loss in the model, most of which is in the earth below the antenna. Losses would mostly go away if we installed a good ground screen below the antenna. We will not do that for now, instead we will assume normal dirt without any large reflector, large counterpoise, ground screen, or radial system to shield the antenna fields from the lossy earth below.
The earth adds about 6 dB or so of ground reflection gain. (At optimum heights, earth can add 6.4 dB gain to make a dipole have ~8.5 dBi gain)
The quad obtains its gain from stacking two bent half-length dipoles 1/4 wave apart. Watch and see how this works!
Stacking Gain and Dipoles
A quad element is really just two bent 1/2 wave elements stacked one above the other. Let's look at gain using two lossless full-size dipoles stacked 1/4 wave apart in freespace:
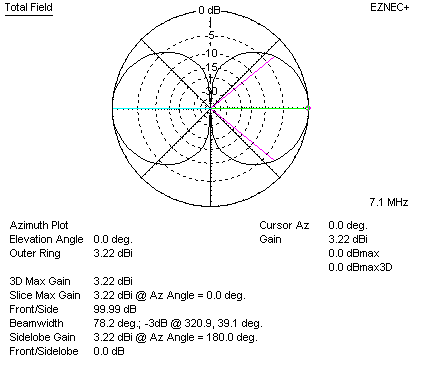
1/4 wavelength is the internal "stacking distance" of a square quad element.
Two dipoles 1/4 wave apart produce enough pattern compression to provide 3.22 dBi total gain. Looking back, the original low-loss dipole in freespace had 2.13 dBi gain. This means the net gain of two full-size stacked dipoles in freespace is 3.22-2.13 = 1.09 dB more than a single dipole. This isn't much gain, and it is an optimum condition (full length elements in freespace) with 1/4 wavelength stacking distance!
Now let's look at the same dipoles over earth, at the same mean height as the original dipole:
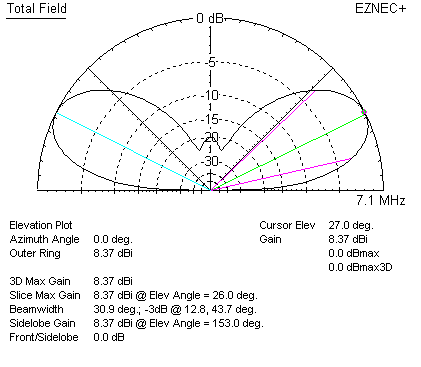
Two dipoles stacked 1/4 wave apart over real earth have 8.37 dBi gain. If we look back, we see a single dipole had 8.09 dBi gain! The net gain from stacking two full-size dipoles 1/4 wave apart over earth, at a mean height of 1/2 wave, is only 0.28 dB! Peak gain wave angle is 27 degrees, a meaningless 1 degree lower than the single dipole.
The earth tries to force an overhead null. The stacked dipole system tries to force a null in the same pattern position! This means at least one of these two effects, both trying to force the same overhead null, cannot give the full gain advantage. Here is the rule for all antennas:
| Rule:
To increase gain, an antenna must force or create a new null in an area of the radiation pattern that previously had significant energy. |
This is always true! Pattern gain increases does not come from adding radiation, gain is produced by removing energy in unwanted directions.
Making gain is very much like squeezing a balloon with a fixed quantity of air to change shape.
Now let's look at a lossless quad loop in space:
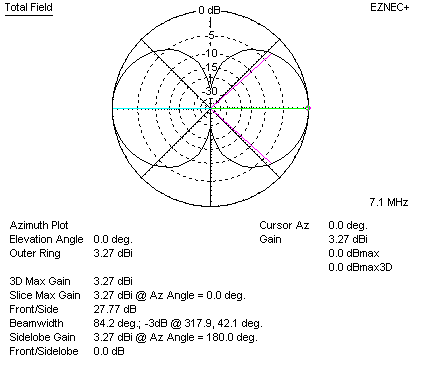
The quad "creates gain" by acting like two half-size end-loaded dipoles stacked one above the other with 1/4 wavelength spacing. In a quad, each bent dipole is 1/4 wave long, and they are 1/4 wave apart.
We now have 3.27 dBi gain, or 1.13 dB more gain than a dipole in freespace. This is a perfect lossless quad element under ideal conditions. Notice this very closely agrees with the gain of two stacked full-length dipoles! In this case it is a little more than 1.09 dB gain, but that is because I made the wires lossless. I wanted to give the quad every possible advantage, so I took away all wire losses.
Now let's look at the quad with copper losses included, over real earth at the same mean height as the dipole:
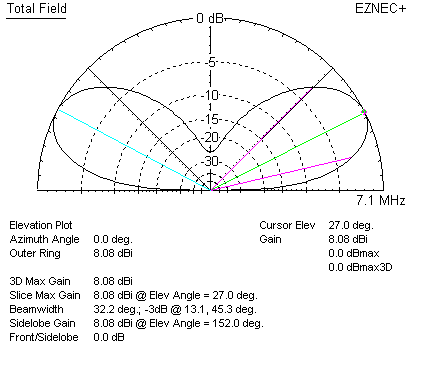
We now have 8.08 dBi gain. The dipole at the same height over the same earth with the same size wire had 8.09 dBi gain. The quad element has 0.01 dB LESS gain than a dipole with the same wire size at the same mean height. Peak radiation occurs at 27 degrees, only one degree less than a dipole!
The quad element has increased the H-plane beamwidth very slightly, and decreased E-plane beamwidth very slightly.
Now in fairness we could have placed the quad element at a height where the earth tries to force a null into an area where the quad has significant energy. Even so, the quad's gain advantage can never be more than the ideal condition of freespace, or just over 1 dB. In reality, the quad advantage is nearly always less than 1 dB over a simple dipole. It's fair and reasonable to say a full wave quad element's gain over a dipole varies from being slightly negative to about 1 dB maximum.
Another common idea or claim is the vertical sides of the quad, with their wide spacing, act like a "leaky transmission line" and allow vertical polarization response simultaneously with the normal horizontally polarized response. The thing that kills this idea are the phase of the vertical-side's currents.
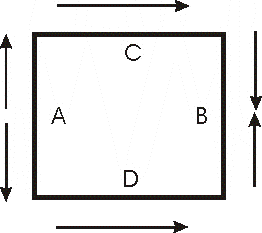
Radiation is caused by charge acceleration, and this means radiation is proportional to current level over distance. It is the ampere-feet that matters. For the horizontally polarized quad element, A and B are at current minimums and contribute minimal radiation.
The side lengths of A and B are also comprised of two 1/8th wave long vertical elements with out-of-phase currents. While side A and side B, like sides C and D, are each a physical total of 1/4 wave, the currents at A and B are both very low and are also out-of-phase. This means we have two small vertical currents on each side flowing opposite directions.
The quad has side-wire radiation cancellation from three effects:
1.) Each side, being short effective lengths and low current, reduces the side ampere-feet and the amount of side radiation
2.) Each side, being out-of-phase with each other, cancels radiation in a broadside direction
3.) The upper and lower halves of each side being out-of-phase, further cancel remaining radiation
If we wanted to do a design that prevents the vertical sides from radiating, the horizontal quad element is an ideal design! C and D essentially do all of the radiating.
What does the above show us?
We have just dispelled four popular quad myths; that a quad element has 2 db gain over a dipole, that a quad is insensitive to height, that a quad has multiple polarizations, and that a quad element or array of elements have a significantly lower radiation-angle than a dipole or an array of dipole elements.
Let's look at a two element quad compared to a two element Yagi at various heights.
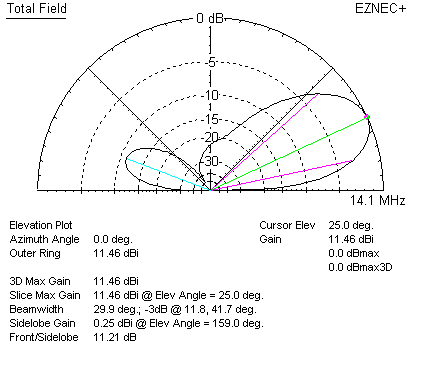
The pattern of left is for a two-element 20-meter quad 35 feet high (1/2 wave high). The antenna is an ARRL Handbook design. This quad has #12 AWG copper elements.
This two-element quad has 11.46 dBi gain, which is about 3 to 3.5 dBd (dB over dipole) gain. This is, unremarkably, about what we would expect from any two-element end-fire array. No magic or enhanced gain here!
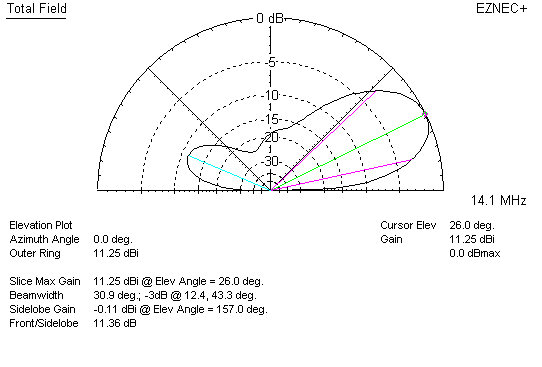
The pattern of a two-element Yagi at the same boom-height as the previously modeled quad, with the same amount of copper in the elements, shows 11.25 dBi gain or 2.7-3.3 dBd (dB over dipole) gain. There is 0.2 db difference between the quad and Yagi using wire elements with the same total copper weight at the same height, in favor of the quad. This very small gain difference is due to slight differences in tuning. Watch what happens when we peak the F/B in the quad by slightly changing reflector size.
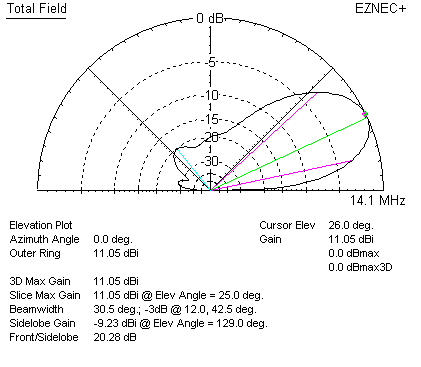
Some adjustment of the quad's reflector from Handbook dimensions improves F/B ratio. Peak F/B ratio is now over 30 dB.
Unfortunately gain has dropped to 11.05 dBi, or about 2.5 to 3 dB over a dipole and less than the Yagi. Once again, this is expected. If we optimize F/B ratio we can expect lower gain from any parasitic array.
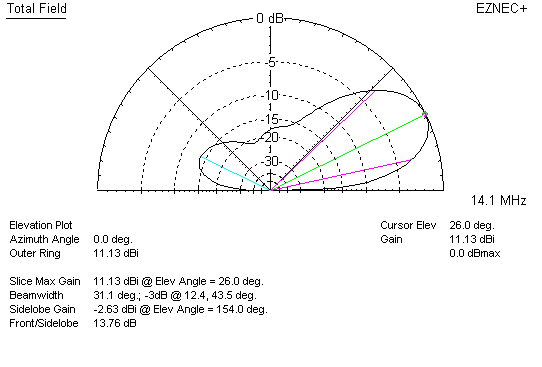
A 2-element Yagi with one-inch diameter tubing elements has about the same gain as a 2-element quad optimized for F/B ratio. They both have the same exact wave angle, dispelling the wave angle myth.
The 2-element Yagi has slightly less F/B ratio, which will slightly impact receiving. If we have unwanted interference or noise from the rear of the antenna the quad will have a slight advantage.
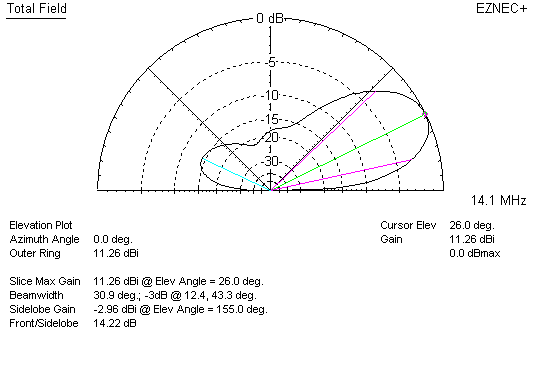
As a matter of fact if we tune the Yagi as a parasitic director instead of reflector, we can shorten the boom to 6 feet, less than half the boom length of the quad, and have about the same performance as the quad!
The clear answer is a two-element quad, all things equal, sometimes offers a slight receiving advantage over the 2-element yagi. This would occur if we have substantial noise or unwanted signals coming from the rear direction. The more elements we add, the less difference in F/B we have. As a matter of fact a 3-element yagi and 3-element quad are essentially equal in gain and F/B ratio. There is virtually no difference between them.
Why is there a big long argument? Because the antennas are so close in performance any real differences are mostly due to construction errors rather than the antenna being a quad or a Yagi!! Use whichever one, quad or Yagi, that you like.
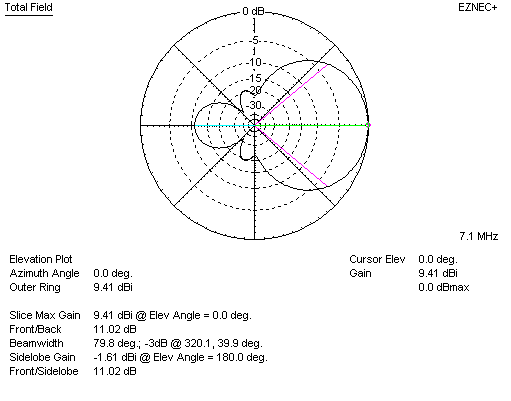
My own 40 meter Yagis, with a 0.4 WL boom, model in freespace to have 9.41 dBi gain at optimum gain frequency.
I chose however to give up a few tenths of a dB gain for higher F/B ratio, bringing them down to just over 9 dBi gain and 28 dB F/B.
Combinations of settings are endless, and I'm sure there are some better than this, but in reality there is very little difference between the quad and yagi antennas. The real difference is mostly in user preference for mechanical attributes.
Keeping it all honest:
Lowering of wave angle? Myth.
2 dB more gain? Myth.
Better receiving? Some truth to that, but the change is small and occurs only under certain conditions.
If we look at antenna books and articles about quad antennas, we will often find references to quad antennas having 2 dB gain over a comparable boom length yagi antenna. The statement often made is a single quad element has 2 dB gain over a dipole, and that 2 dB gain difference carries over into arrays of quad elements. If we actually model or build antennas we find the gain difference between a quad element and dipole is always less than 1.2 dB, and at certain heights a quad element has less gain than a dipole. This makes perfect logical sense. We know a quad element is really two dipoles bent so the ends connect, with 1/4 wave spatial separation between current maximums. This forms a stacked array (broadside array) of two half-size end-loaded dipoles with 1/4 wave spacing. There is a slight increase in E-plane beamwidth by shortening dipole lengths, this tends to reduce gain and broadens the azimuth beamwidth of a horizontally polarized antenna. The stacking gain (broadside gain) tends to slightly compress the H-plane beamwidth of the quad. This effect slightly increases gain. We can look at a graph of broadside gain and see the theoretical maximum stacking gain, even if we do not shorten the radiating area by folding or abruptly bending the ends.
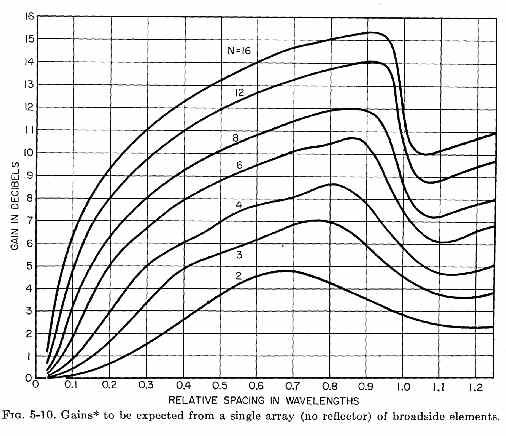
This is no coincidence I invented, or anything new. The graph above is from a 1950's antenna textbook! We can clearly see the gain of two broadside elements 1/4 wave apart is barely over 1 dB, and this is what the antenna models using modern software show. The quad at very best barely has 1 dB gain over a dipole, and at worse has loss. The high current areas just do not have enough spatial separation to provide much gain.
Where did the 2 dB come from then? The first reference I can find to 2 dB gain came in 1952 from Mushiake and Adachi of Tohoku University in Japan. They calculated the gain of a large circular full wave loop as about 2 dBd (dBd = db over dipole). These figures were based on a single circular loop far from ground, not on a square quad loops. The diameter of a 1-wavelength circumference circle is .318 wavelength. We see the theoretical maximum gain is well under 2 dB (even if the elements were dipoles stacked .318 wl apart) and models confirm this. The gain of a circular loop is shown below:
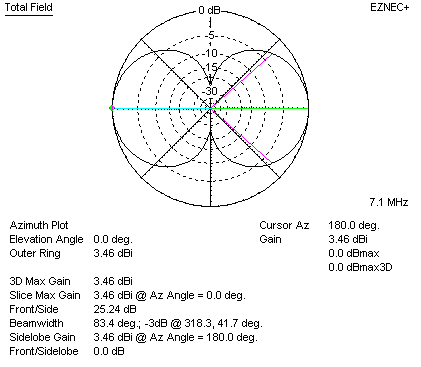
We see the gain of a lossless circular loop is 3.46 dBi, or 1.32 dBd. This is nowhere near the 2 dB put forth by Mushiake and Adachi in 1952. The 1.32 dB NEC model does closely agree with the 1950's engineering textbook. The average or mean separation of the current maximum areas in a full wave circle is about .275 wavelengths, which corresponds to about 1.3 dB gain. Once again the modern NEC-based model and older engineer textbooks closely agree.
It's my belief these measurements carried over into amateur publications and were repeated and exaggerated over the years by well-intentioned but not-so-accurate amateurs.
The first source of amateur measurements I can find were by Lindsey ex-W0HTH (now W7ZQ) on 440 MHz. However derived, these numbers are obviously flawed. 2 db is clearly beyond the highest theoretical maximum ever predicted for circular elements, and his elements were square! Such a mistake is easy to make using measured pattern to estimate gain, which is the method Lindsey used.
The problem is once bad information is printed the misinformation stays in print. We can't go back and erase the May 1968 QST, nor can we erase other publications that copied and reprinted the exaggerated gain claims. The original and copied 2 dBd gain claims will remain in books and archives through eternity. They will reappear as people read old texts and search archives, and the reappearance will fuel the argument that an impossibly flawed gain claim is something "open for debate" because "the argument would not go on for years if the claim did not have merit".
Sorry, but the argument continues only because it once appeared in print and was copied several places. It does not continue because the original exaggerated claims have technical merit.
Some claim a quad element has less noise than a dipole. There is a limited amount of truth to that idea, but not because the antenna is dc grounded and not because it only picks up "magnetic waves"!
DC grounding has no effect, unless something is arcing in the receiver system
or coax. We could for example (in normal weather) just add a shunt choke to a
vertical or a dipole. That would make it "dc grounded", yet doing this
test we find
nothing changes!
We could also use a capacitor. If we added a very low impedance series capacitor
in the "ground path"
side of a loop, nothing happens. Yet the capacitor isolates the loop from dc ground!
The reason for this is simple. DC is not RF.
Noise is not DC. The
receiver already
filters all the
out-of-band noise
out. By definition
we cannot filter
noise except with
selectivity, and
that would require
the antenna be
narrower bandwidth
than the receiver
filters! We know
that isn't true.
There is a very limited amount of truth behind the
"loops are quiet" myth.
The blunt ends of a
quad loop are at the high
impedance voltage
points, rather than
the sharp projected
tips of a Yagi. This can
reduce effects
of precipitation
static....but that
static would only occur
when corona discharge is present at element tips.
The good results with
regard to corona have
nothing at all to do with
dc grounding or any other esoteric loop property. Corona reduction occurs because
the antenna has blunt ends
where high voltage gradients to space around the antenna might, under some
conditions, be present. The
quad loop simply ensures sharp high impedance element ends do not protrude out
into open space! We can do the very same thing with anti-corona balls or rings on the
ends of dipole elements. As a matter of fact this is one reason car antennas
have ball tips. High power CB operators also use anti-corona balls on the tips
of Yagi antennas.
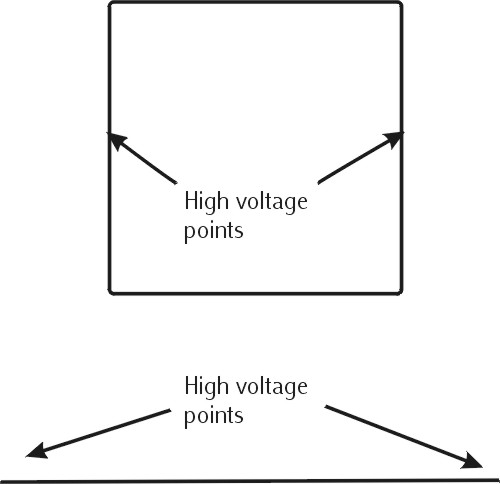
The area most responsive to noise caused by corona discharge is in the center of the blunt sides of a horizontally polarized cubical quad. This is because the highest impedance point in the antenna is at the middle of the blunt sides. The sides are neither the highest point in height (where storm static electric field is most intense) nor are there sharp protruding points.
The area most sensitive to noise caused by corona discharge is at the very tips of a "dipole" style element. Unfortunately this is the highest impedance area, so the very high impedance RF noise caused by corona leakage is matched to the receiver system the best. The tips protrude into empty space away from everything else, and are often at or near the highest point in the antenna. This is where electric field gradient is strongest and corona most likely to form.
Corona Discharge
The Quad was actually popularized in 1942 at radio station HCJB by Clarence Moore. HCJB was a high power shortwave broadcast station located at very high elevations in a humid environment. The environment at HCJB was one of the worst possible locations for a high power transmitting antenna. Regular dipoles would have so much corona from the protruding ends that the dipoles would gradually melt back from the tips, shortening the antenna! The quad reduced E-field gradient at the high voltage points of the antenna while maintaining the same basic pattern and gain as a dipole element. It solved a problem where the antenna tips or ends were charged by a transmitter with very high voltages.
A similar effect occurs when receiving when the environment around the antenna is charged from inclement weather. The very high voltage gradient between the antenna and the air around the antenna causes corona discharge that appears as a hissing, whining, sizzling, or popping noise in the receiver. The most intense charge buildup occurs at the highest point, fartherest from earth and at a point away from other objects in open space. The compact square shape of a quad minimizes protrusions, and places a blunt edge towards the highest charge gradient areas at the top or highest point of the antenna. The yagi or dipole element, on the other hand, has protruding points that extend well out into clear air where charge density and voltage gradient is highest.
During periods of inclement weather when precipitation static is highest, the horizontally polarized quad style element will not only have minimal exposure to high field gradients, the high impedance corona noise will not be as well matched to the receiving system. Less RF energy will be transferred into the system.
Noise and Feedpoint Balance
There is a secondary less commonly thought of reason for less local noise pickup. Many Yagi antennas and dipole antennas have poor baluns or no baluns at all. This leaves the yagi or dipole susceptible to common mode RF pickup on the feed line. This is the electrical equivalent of having a very poor shield on the feed line. The quad, even without a balun, is very much less sensitive to feed line common mode. This is because the quad is not a low impedance source for common mode currents and often cannot drive the shield as effectively as a dipole with common mode currents.
It is from these behaviors, lower noise under conditions of corona discharge in inclement weather and inherently less common mode in a sloppy or poor installation, that exaggerations about "dc grounding" and "closed loops" grew.
Most of the time, if not nearly all of the time, noise plaguing amateurs with properly fed dipoles or quads is from local distant sources. In this case a quad is no quieter than a dipole style element based on element design. If you subscribe to the notion that noise is a different field than signals, that noise is an electric field and signals are a magnetic field and the quad is a "magnetic" antenna, you believe the worse kind of electromagnetic field propagation nonsense. You may want to read other articles about noise, small loop antennas , and electromagnetic fields on this site.
There is one other condition where a 2-element quad might have a slight advantage over Yagi. That would be when strong noises or unwanted signals arrive from the rear, and the quad has been adjusted for maximum F/B ratio. This advantage, like the gain differences, vanish as more elements are added.
as of 1/7/2010 c. W8JI